Thuật toán Tham lam
John Smith đang gặp rắc rối! Anh ấy là một thành viên của Topcoder và sau khi học cách để trở thành bậc thầy trong việc đối phối với các bài toán quy hoạch động, anh ấy bắt đầu giải quyết hàng loạt các bài tập. Nhưng chiếc máy tính "dễ bảo" của anh bắt đầu trở chứng vào hôm nay. Vào mỗi buổi sáng như thường lệ, John thức dậy vào lúc 10 giờ sáng, uống một cốc cà phê và bắt đầu giải các bài tập trước khi thưởng thức bữa sáng. Mặc dù có thứ gì đó "sai sai" so với mọi hôm, nhưng dựa vào kho tàng kiến thức mà anh ấy vừa mới gặt hái được, John đã viết chương trình với một tốc độ thần thánh. Mệt mỏi với việc cấp phát ma trận vào mỗi buổi sáng, chiếc máy tính thông báo rằng: "Segmentation fault!". Dù cho dạ dày còn đang rỗng, song với ý tưởng thông minh của mình, John đã vượt qua rắc rối bằng cách chèn thêm một vòng lặp. Nhưng chiếc máy tính lại gào lên: "Time limit exceeded!".
Thay vì tiếp tục vướng vào mớ rắc rối, John đã có một quyết định thông minh hơn. "Quá đủ cho việc lập trình!" - John nói. Anh ấy quyết định sẽ có một kỳ nghỉ như là phần thưởng cho những nỗ lực của mình.
Là một con người tràn trề sinh lực, John muốn dành thời gian nhiều cho cuộc đời của mình. Có quá nhiều thứ mà anh ta muốn làm, nhưng không may là anh ta không thể nào làm hết tất cả chúng được. Thế nên trong lúc ăn sáng, John đã vạch ra một "Fun plan" được thể hiện bằng một thời gian biểu cho từng hoạt động như sau:
| Id | Hoạt động | Thời gian |
|---|---|---|
| 1 | Sửa phòng | Thứ 2, 22:00 đến thứ 3, 1:00 |
| 2 | Du lịch Hawaii | Thứ 3, 6:00 đến thứ 7, 22:00 |
| 3 | Vô địch cuộc thi cờ vua | Thứ 3, 11:00 đến thứ 3, 21:00 |
| 4 | Thạm dự nhạc hội Rock | Thứ 3, 19:00 đến thứ 3, 23:00 |
| 5 | Chiến thắng cuộc thi Starcraft | Thứ 4, 15:00 đến thứ 5, 15:00 |
| 6 | Chơi trò bắn súng nước sơn | Thứ 5, 10:00 đến thứ 5, 16:00 |
| 7 | Tham gia kỳ thi SRM trên Topcoder | Thứ 7, 12:00 đến thứ 7, 14:00 |
| 8 | Tắm rửa | Thứ 7, 20:30 đến thứ 7, 20:45 |
| 9 | Tổ chức tiệc ngủ | Thứ 7, 21:00 đến Chủ nhật, 6:00 |
| 10 | Tham gia thử thách "All you can eat" và "All you can drink" | Thứ 7, 21:01 đến thứ 7, 23:59 |
Giờ anh ấy muốn thực hiện được tối đa các hoạt động trong thời gian biểu trên. Mặc dù để lên kế hoạch hiệu quả thì cần phải có chút lý trí, nhưng giờ thì hồn anh ấy đã đắm chìm vào kỳ nghỉ rồi.
Liệu ta có thể giúp anh ấy có một kỳ nghỉ tuyệt vời? Ta hoàn toàn có thể! Đầu tiên, ta hãy đưa ra một giả định. Là một lập trình viên tỉ mỉ, một khi đã đặt ra kế hoạch, anh ấy buộc phải thực hiện nó. Thế nên, mỗi hoạt động chỉ có hai chọn lựa là có hoặc không. Và với mỗi trường hợp chọn lựa cho hoạt động thứ nhất, ta lại có thêm 2 lựa chọn cho hoạt động thứ 2. Phân tích nhanh ta sẽ thấy được rằng có $2^n$ trường hợp, và trong tình huống này thì đó sẽ là $2^{10} = 1024$ trường hợp. Với mỗi trường hợp ta sẽ kiểm tra xem nó có thỏa mãn giới hạn về thời gian hay không. Từ đây, việc cho lựa 1 phương án có nhiều hoạt động nhất sẽ trở nên dễ dàng hơn. Với khá nhiều sự chọn lựa như thế này, John buộc phải nhờ đến sự giúp đỡ của chiếc máy tính đang mệt mỏi. Nhưng điều gì sẽ xảy ra nếu John có tới 50 hoạt động trong danh sách? Thậm chí dùng đến cả siêu máy tính nhanh nhất thế giới thì cũng cần đến vài năm để tìm ra câu trả lời. Thế nên, phương án này khá phi thực tế.
Chúng ta hãy cùng tìm cách đơn giản hóa vấn đề. Một phương án tốt có lẽ là thực hiện công việc ngay khi thời cơ đến: Nếu ta có hai hoạt động và chúng bị trùng về thời gian, ta sẽ ưu tiên lựa chọn hoạt động xảy ra trước nhằm tiết kiệm thời gian. Ví dụ trong trường hợp anh ta bắt đầu buổi tối đầu tiên bằng việc sửa chữa phòng. Buổi sáng, anh ấy sẽ bắt một chuyến bay. Và chưa đầy một ngày nhưng anh ấy đã thực hiện được 2 hoạt động. Thật tuyệt vời! Nhưng thật ra, đó chỉ là lựa chọn tốt nhất lúc này thôi. Và bây giờ thì ta có gì, 5 ngày ăn chơi ở Hawaii và cho đến tận tối thứ 7 thì anh ấy vẫn chỉ thực hiện được 2 hoạt động. Hãy nghĩ xem trong 5 ngày đó anh ta đã có thể thực hiện được những gì. Mặc dù đơn giản và thực thi rất nhanh, song rất không may là thuật toán này lại không chính xác.
Ta vẫn không cần phải xét tất cả các trường hợp, hãy thử một mánh khóe khác. Giờ ta sẽ bỏ những hoạt động tiêu tốn nhiều thời gian như đi du lịch Hawaii bằng cách lựa chọn những hoạt động tốn ít thời gian nhất và kiểm tra xem nó có hợp lí với những hoạt động đã chọn trước đó chưa rồi tiếp tục quá trình. Theo như thời gian biểu ở trên thì hoạt động đầu tiện được chọn lựa sẽ là tắm. Với thời gian chỉ 15 phút, đây chính là lựa chọn cục bộ tối ưu. và giờ điều mà ta cần biết đó là có thể giữ được tối ưu cục bộ khi mà những hoạt động thích hợp khác được chọn lựa. Thời gian biểu của John sẽ như sau:
- Đi tắm (15 phút).
- Tham gia vào kỳ thi SRM trên Topcoder (2 tiếng).
- Tham gia thử thách "All you can eat" và "All you can drink" (2 tiếng 58 phút).
- Sửa phòng (3 tiếng).
- Tham nhạc buổi hòa nhạc Rock (4 tiếng).
- Chơi bắn súng nước sơn (6 tiếng).
Trong 10 hành động, ta đã lựa ra được 6 hành động (hoàn toàn không tệ). Giờ thì thuật toán của ta đã chậm lại nhưng nó trở nên đáng tin cậy hơn nếu đây là lựa chọn tốt nhất mà ta có thể thực hiện. Và quả thực, đáp án chính là 6. John rất hài lòng về sự hỗ trợ của chúng ta, nhưng sau khi trở về từ kỳ nghỉ với kế hoạch thông minh này, John đã phải đối mặt với những rắc rối nghiêm trọng khác:
Áp dụng thuật toán của ta, John đã tham gia một cuộc hẹn hò chóng vánh, để rồi anh ấy đã bỏ lỡ cả bài thi trong trường lẫn trận đấu bóng rổ của đội anh ấy yêu thích. Là một Topcoder, chúng ta cần phải viết ra một chương trình hoàn toàn có thể tin cậy trong vấn đề này. Chỉ cần một trường hợp duy nhất chúng ta không giải quyết được sẽ dẫn tới một thất bại toàn diện.
Những gì mà chúng ta thường làm trong tình huống này là phân tích điều gì đã gây ra lỗi ở lựa chọn đầu tiên và các hành động phù hợp để tránh nó trong tương lai. Giờ ta hãy xét lại kịch bản đầu tiên. Cuộc hẹn hò trùng thời gian với cả việc làm bài thi lẫn trận đấu bóng rổ, trong khi cả trận đấu bóng rổ lẫn làm bài thi chỉ trùng lặp với một mình cuộc hẹn hò. Vậy thì ý tưởng cũng tự sinh ra từ vấn đề này. Tại sao ta không chọn hoạt động ít bị trùng lặp nhất so với những hoạt động còn lại ? Nghe có vẻ hợp lí - giờ thì một thứ đã đúng hơn rồi đấy ! Giờ ta sẽ thử chứng minh rằng phương pháp này hoàn toàn đúng đắn. Giờ giả sử ta đã lựa chọn hoạt động X, ta se thử kiểm tra xem ta có thể lựa chọn hoạt động A và B (những hoạt động bị trùng lặp với X) thay vì X được hay không. Và A, B cũng không được trùng lặp nhau, nếu không ta cũng không thể tối ưu hóa kết quả. Bây giờ, ta sẽ quay về trường hợp trước đó (X trùng với 2 hoạt động, A và B trùng với 1 hoạt động). Trong trường hợp này, ta sẽ chọn A và B ngay từ đầu tiên. Một trong những cách để phản bác lại giả thiết này chính là cho hoạt động A và B trùng lặp với nhiều hoạt động hơn nữa chứ không chỉ hoạt động X. Nghe nó có vẻ không trực quan cho lắm, nhưng (thật không may) ta vẫn có thể xây dựng trường hợp đó như sau:

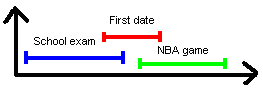
Nhưng hoạt động được biểu diễn bằng gạch màu xanh chính là những lựa chọn tối ưu trong thời gian biểu trên. Nhưng hoạt động tô màu đỏ trùng lặp với 2 hoạt động nên nó sẽ được chọn trước. Vẫn còn 4 hoạt động thích hợp khác trước hoạt động đỏ, nhưng chúng đều bị trùng lặp lẫn nhau, thế nên ta chỉ có thể lựa chọn thêm 1 hoạt động. Điều tương tự cũng xảy ra đối với 4 hoạt động sau hoạt động màu đỏ, nhưng ta vẫn chỉ có thể chọn 1. Vậy tổng cộng theo phương pháp này, ta vẫn chỉ có thể chọn 3 hoạt động, trong khi kết quả tối ưu là 4.
Tổng quát lại, ta thấy được rằng mỗi đáp án của chúng ta đều tồn tại một thiếu sót. Có vẻ như chúng ta đang đối mặt với một vấn đề hóc búa. Nhưng thật ra, vấn đề này vẫn có một cách giải quyết đẹp đẽ, và không hề phức tạp. Nếu ta xem xét các hình trên một cách kỹ lưỡng hơn nữa, ta sẽ thấy được rằng hoạt động màu xanh nằm ở góc trái dưới là là hoạt động duy nhất hoàn thành trước "timeline" được biểu diễn bằng đường vẽ dọc màu đỏ. Vậy, nếu lựa chọn 1 hoạt động đơn lẻ, ta sẽ chọn hoạt động kết thúc đầu tiên (tại thời điểm t1), lúc đó toàn bộ khoảng thời gian còn lại sẽ trống để ta có thể chọn các hoạt động khác. Nếu chúng ta chọn bất kỳ hoạt động nào khác, thì khoảng thời gian còn lại sẽ ngắn đi. Điều này là hiển nhiên, bởi vì khi ta kết thúc với bất kỳ một hoạt động nào khác thì luôn luôn t2 > t1. Trong trường hợp đầu tiên, ta sẽ có toàn bộ thời gian từ t1 đến khi kết thúc và bao gồm luôn khoảng từ t2 đến kết thúc. Bởi vậy mà nó cũng không có khuyết điểm trong việc lựa chọn hoạt động kết thúc sớm. Và nó còn có một ưu điểm đó là ta hoàn toàn có thể chèn thêm một hoạt đồng bất kỳ vào giữa t1 và t2 và kết thúc trước khi hoạt động của t2 bắt đầu.
Được biết tới với tên gọi "Lựa chọn hoạt động", đây là bài toán cơ sở sử dụng "Phương pháp Tham lam". Giống như là một gã tham lam luôn muốn chiếm lấy nhiều nhất, thường xuyên nhất mà hắn ta có thể, trong trường hợp này, ở mỗi bước ta sẽ chọn lựa một hoạt động kết thúc đầu tiên và mỗi lần đều không có hoạt động đang trong tiến trình. Và có một sự thật đó là ta luôn luôn áp dụng phương pháp tham lam cho mỗi bước trong cuộc đời của mình. Khi ta đi mua sắm hoặc đi xe hơi, ta đều luôn lựa chọn phương án tốt nhất tại thời điểm hiện tại. Thật ra, phương pháp tham lam có 2 công thức chung: * Tính lựa chọn tối ưu: Từ những kết quả tối ưu cục bộ ta có thể đi đến kết quả tối ưu toàn cục mà không cần phải xem xét lại các kết quả. * Tính tối ưu từ bài toán nhỏ: Kết quả tối ưu có được xác định bằng các kết quả tối ưu từ bài toán nhỏ hơn.
Đoạn mã giả dưới đây diễn ta cách lựa chọn tối ưu các hoạt động bằng thuật toán tham lam mà ta vừa chứng minh phía trên:
Đặt N là số hoạt động và
{I} là hoạt động thứ I (1 <= I <= N)
Với mỗi {I}, xét S[I] và F[I] lần lượt là thời gian bắt đầu và kết thúc của hoạt động đó.
Sắp xếp lại các hoạt động theo thứ tự tăng dần của thời gian kết thúc.
- Có nghĩa là, với I < J ta phải có F [I] <= F [J]
// A là tập hợp các hoạt động được chọn
A = {1}
// J là hoạt động cuối cùng được chọn
J = 1
For I = 2 to N
// ta có thể chọn I nếu nó là hoạt động cuối cùng
// việc chọn lựa đã hoàn thành
If S [I] >= F [J]
// lựa chọn hoạt động 'I'
A = A + {I}
// hoạt động 'I' giờ trở thành hoạt động cuối cùng được lựa chọn
J = I
Endif
Endfor
Return ASau khi áp dụng thuật toán trên, "Fun plan" của Johnny sẽ như thế này:
- Xóa hết mọi lỗi và đi tắm.
- Thứ 3 để đánh cờ và chiến thắng.
- Cả ngày để chơi Starcraft, có vẻ vui đây.
- Hai ngày tiếp theo để nghỉ ngơi.
- Và vào ngày cuối cùng, lấy một ít điểm rating từ Topcoder, tắm rửa, tận hưởng bữa ăn "sâu bọ" và những ly rượu hảo hạng.
Vấn đề của John Smith đã được giải quyết, tuy nhiên đây chỉ là một ví dụ mà Tham lam có thể hoạt động. Một vài vấn đề thật sự khác đến từ Topcoder sẽ giúp bạn hiểu rõ hơn về khái niệm này. Trước khi tiếp tục, có lẽ bạn cần phải luyện tập thêm chút ít nữa với những gì mà bạn vừa đọc, bằng bài tập tương tự với Lựa chọn hành động, tên là Boxing
BioScore
Đối với bài tập này, bạn sẽ được yêu cầu làm tối đa hóa số điểm trung bình của các cặp tương đồng. Từ đáp án tối ưu cần tìm, ta có thể xem nó như một gợi ý nhằm giúp ta tìm ra phương án thích hợp. Thường thì, đối với dạng bài toán này, ta sẽ sử dụng phương pháp quy hoạch động để giải quyết, nhưng trong một vài trường hợp thì chiến lược Tham lam vẫn hoàn toàn có thể được sử dụng.
Việc đầu tiên mà ta cần làm là xây dựng một ma trận cho biết số lần lặp (ma trận tần số). Đây là một công việc khá nhẹ nhàng khi mà ta chỉ cần ghép từng cặp ký tự ở hai chuỗi tạo thành một axit nucleic rồi đếm số lần xuất hiện của chúng (AA, AC, AG, AT, CA, CC, CG, CT, GA, GC, GG, GT, TA, TC, TG, TT). Từng loại axit nucleic sẽ được xem như một phần tử trong ma trận và giá trị của nó chính là số lần xuất hiện của nó. Ví dụ, hãy xét bộ {"ACTAGAGAC", "AAAAAAAAA", "TAGTCATAC", "GCAGCATTC"} được sử dụng ở ví dụ thứ 2.
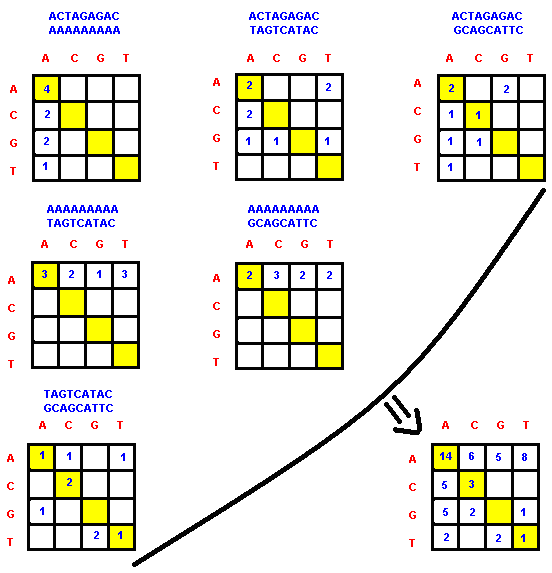
Ở góc phải - dưới của hình minh họa trên, ta có thể thấy kết quả của ma trận tần số đối với bộ đã cho. Tạm gọi nó là F. Giờ việc mà ta cần làm là tìm ra một ma trận S khác sao cho tổng của các tích số của 16 loại axit nucleic $F[i, j]*S[i, j]$ $(1 \le i, j \le 4)$ là lớn nhất.
Giờ ta xét từng điều kiện cho ma trận cần tìm:
1) Tổng của 16 phần tử bằng $0$:
Đây là một điều kiện khá phổ biến. Bởi tất cả các phần tử của F đều dương (em nghĩ là không âm chứ?), nên các điểm cuối cùng có xu hướng tăng khi ta tăng phần tử của S. Nhưng bởi vì tống của chúng phải bằng $0$, thế nên khi ta tăng giá trị 1 phần tử lên thì ta sẽ phải giảm đi giá trị của 1 phần tử khác. Thử thách ở điều kiện này chính là phải tìm ra một sự phân bố tối ưu.
2) Giá trị mỗi phần tử chỉ nằm trong khoảng từ -10 đến 10 ($S[i, j] \in [-10, 10]$)
Lại một điều kiện phổ biến khác! Với điều kiện này, khoảng tìm kiếm của chúng ta đã được thu hẹp đi rất nhiều, song vẫn còn khá nhiều lựa chọn cho ta.
3) Mỗi phần tử đối xứng phải có giá trị bằng nhau ($score(x, y) = score(y, x)$)
Bởi vì tính đối xứng, ta phải quy định cho các điểm cho các cặp như "AC" và "CA" bằng nhau. Như là một hệ quả, ta đã vô tình đếm số lần xuất hiện của chúng. Đối với ví dụ trên, ta đã có tần số của tập hợp các cặp như sau:
| AA: 14 | CC: 4 | GG: 0 | TT: 1 |
| AC+CA: 11 | AG+GA: 10 | AT+TA: 10 | |
| CG+GC: 2 | TC+CT: 0 | ||
| GT+TG: 3 |
Từ trực giác ta có thể thấy ngay đến phương án như sau: đã sẽ gán điểm số càng cao đối với cặp xuất hiện càng nhiều lần. Tuy nhiên, ta lại bị ràng buộc rằng tổng các phần tử phải bằng 0, một vấn đề khác lại nảy sinh. Những cặp như AA, CC, GG, TT chỉ xuất hiện một lần trong ma trận nên số điểm của chúng sẽ ít hơn so với tổng điểm.
4) Các phần tử trên đường chéo phải dương ($score(x, x) > 0$)
Sự khác biệt giữa các phần tử trên đường chéo và các phần tử còn lại ngày càng lớn. Nhìn chung, ta có hai loại phần tử: bốn phần tử trên đường chéo (các phần tử đại diện cho AA, CC, GG, TT) và sáu phần tử không nằm trên đường chéo (các phần tử đại diện cho AC + CA, AG + GA, AT + TA, CG + GC, CT + TC, GT +TG). Mỗi nhóm trên sẽ có các cấu hình khác nhau, tùy thuộc vào cách mà ta đặt giá trị cho chúng.
Đơn giản hóa vấn đề, với mỗi cấu hình ta đặt nhóm thứ nhất, ta sẽ tìm ra đáp án tối ưu cho nhóm thứ hai. Bởi vì tất cả các phần tử ở nhóm thứ hai đều có chung tính chất, ta sẽ sử dụng phương pháp Tham lam để tìm kết quả tối ưu cho nhóm thứ hai. Nhưng vì mỗi giá trị ở nhóm thứ nhất đều có thể chọn trong khoảng $[1, 10]$, nên giá trị tổng mà ta tìm kiếm ở nhóm hai cần phải được tính toán lại. Không khó để nhận ra tổng của nhóm thứ nhất có thể là bất kỳ số nào trong khoảng $[4, 40]$. Như một hệ quả, dựa vào việc ta chọn tổng ở nhóm một, ta có thể suy ra được tổng của nhóm hai sẽ trong khoảng $[-20, -2]$ (chúng ta không được quên rằng nhóm hai đối xứng, xuất hiện hai lần trong ma trận nên giá trị phải nhân đôi lên).
Và giờ, ta đã đến được cốt lõi của vấn đề. Lời giải cho cả vấn đề này chính là việc tìm được giá trị điểm tối ưu cho nhóm thứ hai. Nếu vấn đề quả thật là lựa chọn tham lam và tối ưu hóa cục bộ, ta hoàn toàn có thể lấy một phần tử ra, gắn cho nó giá trị tối ưu và thực hiện tương tự với các phần tử còn lại.
Ta có được khẳng định như sau: Nếu ta luôn luôn gán giá trị lớn nhất có thể cho phần tử xuất hiện nhiều lần nhất trong một nhóm, và cuối cùng ta sẽ thu được kết quả lớn nhất có thể cho toàn nhóm đó.
Việc đầu tiên mà ta cần làm là sắp xếp lại sáu phần tử này trong ma trận F. Giờ, ta sẽ thực sự tính toán các giá trị tương ứng trong S. Tổng điểm tối thiểu mà ta đạt được là $-20$, một ý nghĩ chợt lóe lên trong ta, hai giá trị đầu tiên sẽ được gắn bằng $10$ (kể cả 4 giá trị còn lại ta có gán $-10$ đi chăng nữa thì ta vẫn thu về được giá trị $-20$). Ta biến rằng số điểm cuối cùng sẽ nhỏ hơn $0$. Bởi vì ta muốn tối đa hóa số điểm của phần tử đầu tiên nên ba phần tử còn lại sẽ là $-10$ (trong trường hợp tốt nhất, điểm tổng sẽ là $-2$ và lúc đó, ta sẽ điền số điểm như sau: $[10, 10, 8, -10, -10, -10]$). Cuối cùng, giá trị của phần tử thứ ba sẽ được xác định dựa vào lựa chon của ta cho nhóm thứ nhất. Đối với giá trị lớn nhất là $10$, ta sẽ trừ đi phần nửa của tổng số điểm của nhóm thứ nhất (ta lưu ý rằng tổng nói trên buộc phải là số chẵn).
Giờ thì ta cần phải chứng minh rằng phương pháp của mình là đúng. Cách chứng mình này cũng không quá phức tạp. Nhằm mục đích để tổng của S là một hằng số, ta chỉ có thể giảm các cặp có số lần xuất hiện nhiều hơn tăng những cặp có số lần xuất hiện ít hơn. Gọi f1 và f2 lần lượt là số lần xuất hiện của của hai cặp và $f1 \ge f2$. Ta có $f1 * s1 + f2 * s2 = X$, với X là tổng tối đa mà ta đạt được. Bằng giả định Tham lam của ta, $s1 \ge s2$. Vì tổng $s1+s2$ là một hằng số, tổng trên sẽ biến đổi thành $f1 * (s1-a) + f2 * (s2-a) = Y$ với a là số dương ($a > 0$). Ta tìm ra được rằng $Y-X = a * (f2-f1)$. Bởi vì $f1 \ge f2$ nên khoảng cách này luôn dương. Vì Y có thể lựa chọn tùy ý, ta có thể kết thúc lựa chọn Tham lam ban đầu bằng việc luôn cho Y số điểm lớn nhất.
Ta áp dụng thuật toán trên cho mỗi cấu hình của các phần tử trong nhóm đầu tiên và lưu lại kết quả tốt nhất.
Phương pháp biểu diễn: Thay vì phải dùng tới hai ma trận F và S, ta có thể dùng một mảng đề lưu đồng thời cả cả số lần lặp lẫn số điểm tương ứng. 4 phần tử đầu tiên của mảng F sẽ thể hiện tần số của các cặp AA, CC, GG, TT. 6 phần tử tiếp theo sẽ lưu số lần lặp của các cặp có thể sinh ra và được sắp xếp giảm dần dựa vào tần số $(F[5] \ge F[6] \ge F[7] \ge F[8] \ge F[9] \ge F[10])$. S sẽ là một mảng có 10 phần tử mà $S[i]$ chính là số điểm mà ta phân bổ cho cặp $i$.
Ý tưởng chính của thuật toán trên sẽ được minh họa trong đoạn mã giả dưới đây:
Best = -Infinity
For S [1] = 1 to 10
For S [2] = 1 to 10
For S [3] = 1 to 10
For S [4] = 1 to 10
If (S [1] + S [2] + S [3] + S [4]) mod 2 = 0
S [5] = S[6] = 10
S [7] = 10 - (S [1] + S [2] + S [3] + S[4]) / 2
S [8] = S [9] = S [10] = -10
// biến Best sẽ lưu lại giá trị trung bình lớn nhất
Best = max (Best , score (F,S))
// kết quả tốt nhất thu được đến lúc này
Endif
Endfor
Endfor
Endfor
Endfor
Return BestĐối với mảng lưu điểm đã cho (trong trường hợp của chúng ta là mảng S), ta sẽ tính kết quả cuối cùng bằng việc chỉ tính tổng của tích $F[I] * S[I] (1 \le I \le 10)$ và chia nó cho $N * (N-1) / 2$ để thu được kết quả trung bình.
GoldMine
Giờ ta sẽ đi tìm hiểu xem bằng cách nào một mỏ vàng có thể bị khai thác triệt để, bằng việc sử dụng phương pháp Tham lam. Mỗi khi ta nhận ra có sự liên quan tới lợi nhuận tối đa, thì khi đó, phương pháp Tham lam sẽ được sử dụng. Trong trường hợp này, ta sẽ chỉ định những người đào vàng đến các mỏ vàng sao cho tổng lợi nhuận thu được là tối đa. Phân tích nhanh, ta nhận ra rằng cần phải biết lợi nhuận thu được từ một mỏ trong tất cả các trường hợp. Và nó cũng không có nhiều trường hợp cho lắm. Với một mỏ bất kỳ, ta chỉ có từ 0 đến 6 người đào mỏ. Bảng dưới đây sẽ cho ta thấy lợi nhuận khả thi đối với hai mỏ ở ví dụ 0 trong bài:
| 0 người | 1 người | 2 người | 3 người | 4 người | 5 người | 6 người | |
| Mỏ 1 | $0$ | $57$ | $87$ | $87$ | $67$ | $47$ | $27$ |
| Mỏ 2 | $0$ | $52$ | $66$ | $75$ | $75$ | $66$ | $48$ |
Bởi nhiệm vụ ta cần làm là phân công các người đào mỏ, nên ta cần phải biết được lợi nhuận mà một người đào mỏ mang đến với mỏ mà anh ta được phân công. Nếu ta chỉ có duy nhất một người đào mỏ, lựa chọn tối ưu chính là chính là cho anh ta vào mỏ nơi mà anh ta mang lại nhiều lợi nhuận nhất. Nhưng nếu ta có nhiều người đào mỏ, ta cần phải kiểm tra xem nếu phân công anh ở mỏ tương tự có mang lại lợi nhuận cục bộ tối ưu không.
Trong ví dụ, ta có 4 người đào mỏ cần được phân công. Bảng dưới đây sẽ cho biết lợi nhuận thu được của mỗi mỏ với từng người đào mỏ được thêm vào.
| Ban đầu | Người 1 | Người 2 | Người 3 | Người 4 | Người 5 | Người 6 | |
| Mỏ 1 | $-$ | $57$ | $30$ | $0$ | $-20$ | $-20$ | $-20$ |
| Mỏ 1 | $-$ | $52$ | $14$ | $9$ | $ 0$ | $-9 $ | $-20$ |
Ta để ý rằng, mỏ 1 sẽ tăng thêm 57 nếu ta thêm vào 1 người đào mỏ, trong khi mỏ 2 chỉ tăng thêm 52. Thế nên, ta sẽ phân bố người đầu tiên vào mỏ 1.
| Ban đầu | Người 1 | Người 2 | Người 3 | Người 4 | Người 5 | Người 6 | |
| Mỏ 1 | $-$ | $57$ | $30$ | $0$ | $-20$ | $-20$ | -20 |
| Mỏ 1 | $-$ | $52$ | $14$ | $9$ | $ 0$ | $-9 $ | $-20$ |
Giờ, nếu ta thêm người đào mỏ vào mỏ 1, ta chỉ tăng lợi nhuận được thêm 30. Bởi vậy nên ta sẽ thêm người đào mỏ vào mỏ mỏ 2, lúc này lợi nhuận ta thu được sẽ tăng thêm 52.
| Ban đầu | Người 1 | Người 2 | Người 3 | Người 4 | Người 5 | Người 6 | |
| Mỏ 1 | $-$ | $57$ | $30$ | $0$ | $-20$ | $-20$ | $-20$ |
| Mỏ 1 | $-$ | $52$ | $14$ | $9$ | $0$ | $-9 $ | $-20$ |
Người đào mỏ thứ 3 sẽ hữu ích hơn khi làm ở mỏ 1 với lợi nhuận thu được là 30.
| Ban đầu | Người 1 | Người 2 | Người 3 | Người 4 | Người 5 | Người 6 | |
| Mỏ 1 | $-$ | $57$ | $30$ | $0$ | $-20$ | $-20$ | $-20$ |
| Mỏ 1 | $-$ | $52$ | $14$ | $9$ | $0$ | $-9$ | $-20$ |
Với người đào mỏ thứ 4, ta có thể cho anh ta vào mỏ 1 (với lợi nhuận là 0) hoặc mỏ 2 (với lợi nhuận là 14). Dễ thấy, ta sẽ phân công anh ấy vào mỏ hai.
| Ban đầu | Người 1 | Người 2 | Người 3 | Người 4 | Người 5 | Người 6 | |
| Mỏ 1 | $-$ | $57$ | $30$ | $0$ | $-20$ | $-20$ | $-20$ |
| Mỏ 1 | $-$ | $52$ | $14$ | $9$ | $0$ | $-9$ | $-20$ |
Cuối cùng, hai người đào mỏ còn lại sẽ được phân công bằng cách cho cả hai vào làm ở mỏ 2 hoặc mỗi người làm ở một mỏ riêng. Ví dụ cho ta thấy kết quả mà ta vừa tìm được quả thực chính là kết quả tối ưu. Nhưng phương pháp Tham lam của chúng ta có luôn luôn hoạt động không?
Khẳng định: Ta luôn luôn thu được tổng lợi nhuân lớn nhất khi lần lượt cho từng người đào mỏ vào mỏ có lợi nhuận cao nhất ở thời điểm hiện tại.
Chứng minh: Gọi $A, B$ lần lượt là mỏ 1 và mỏ 2, $a1, b1, a2, b2$ được định nghĩa như sau:
$a1$ - lợi nhuận thu được khi phân công thêm một người đào mỏ vào $A$.
$a1+a2$ - lợi nhuận thu được khi phân công thêm hai người đào mỏ vào $A$.
$b1$ - lợi nhuận thu được khi phân công thêm một người đào mỏ vào $B$.
$b1+b2$ - lợi nhuận thu được khi phân công thêm hai người đào mỏ vào $B$.
Thuật toán Tham lam của ta sẽ gia tăng lợi nhuận bằng $a1$ cho người đào mỏ đầu tiên và $(a2+b1)$ cho người đào mỏ thứ 2. Tổng lợi nhuận lúc này sẽ là $a1+max(a2, b1)$. Nếu ban đầu ta chọn $b1$ thì lợi nhuận của người đào mỏ thứ 2 thu được sẽ là $a1$ hoặc $b2$.
Trong trường hợp đầu tiên, ta sẽ có $a1+b1 \le a1+max(a2, b1)$.
Trong trường hợp thứ hai, tổng lợi nhuận sẽ là $b1+b2$. Ta cần phải chứng minh $b1+b2 \le a1+max(a2, b1)$. Mà ta luôn có $b1 \le b2$ vì lợi nhuận thu được từ việc thêm một người đào mỏ vào một mỏ luôn luôn lớn hơn hoặc bằng lợi nhuận thu được từ việc thêm một người đào mỏ nữa vào mỏ đó.
| Trạng thái của mỏ vàng | Lợi nhuận từ việc thêm 1 người | Lợi nhuận từ việc thêm 1 người |
| Số lượng mỏ $>$số lượng người đào+2 | $60$ | $60$ |
| Số lượng mỏ $=$ số lượng người đào+2 | $60$ | $50$ |
| Số lượng mỏ $=$ số lượng người đào+1 | $50$ | $-20$ |
| Số lượng mỏ $<$ số lượng người đào+2 | $-20$ | $-20$ |
Vì $b1+b2 \le a1+a2 \le a1+b1 \le a1+max(a2, b1)$, lựa chọn Tham lam cũng chính là phương án tối ưu.
Lập trình nó hoàn toàn không khó, nhưng ta cần phải xử lý thêm các trường hợp nữa (tất cả các người đào mỏ đều phải được phân công, chỉ có tối đa sáu người trong một mỏ và nếu một người đào mỏ có thể được đặt tối ưu ở nhiều mỏ, ưu tiên mỏ có chỉ số nhỏ hơn).
WorldPeace
Những thuật toán Tham lam mà ta vừa kể trên đều hoạt động tốt ở mọi tình huống bởi sự đúng đắn của nó đã được ta chứng minh. Nhưng còn một lớp bài tập tối ưu hóa nữa mà thuật toán Tham lam có thể được áp dụng. Đây là những bài tập thuộc lớp NP - đầy đủ (như bài toán người đưa thư TSP Traveling Salesman Problem), và người ta thường viết các nhánh - cận dựa trên Tham lam hơn là chờ đợi chương trình thực thi... Lời giải không phải lúc nào cũng là tối ưu, song đối với phần lớn mục đích, thì nó đã đủ tốt rồi. Nếu đây không phải là một bài toán lớp NP, thì nó chính là một ví dụ tuyệt vời cho việc một thuật toán Tham lam không chỉ có thể đánh lừa và vượt qua các test mẫu, mà nó còn có thể vượt qua cả những bộ test hệ thống được thiết kế kỹ càng. Và thuật toán này thật sự không quá khó để nghĩ ra, mà chỉ cần một vài phân tích nhanh ta có thể nhận ra để tối đa hóa tổng số lượng nhóm, luôn luôn tối ưu để tạo thiết lập một nhóm từ k quốc gia có dân số đông nhất. Chúng ta áp dụng phương pháp này ở từng bước và sau đó sắp xếp lại đoạn để thấy được k quốc gia tiếp theo có dân số đông nhất. Ý tưởng này sẽ được minh họa trong đoạn mã giả dưới đây:
Groups = 0
Repeat
// sắp xếp lại mảng theo thứ tự giảm dần
Sort (A)
Min= A[K]
If Min > 0 Groups = Groups + 1
For I = 1 to K
A[I] = A[I] - 1
Endfor
Until Min = 0
Return GroupsKhông may thay, mỗi quốc gia lại có tới hàng tỷ người dân, thế nên ta không thể nào thiết lập từng nhóm một được. Về mặt lý thuyết, đối với một tập hợp của k quốc gia, chúng ta sẽ tạo nhóm cho đến khi mà toàn bộ người dân của nước đó đã được phân nhóm. Và điều này sẽ được thực hiện chỉ trong 1 bước:
Groups = 0
Repeat
// sắp xếp lại mảng theo thứ tự giảm dần
Sort (A)
Min= A[K]
Groups = Groups + Min
For I = 1 to K
A[I] = A[I] - Min
Endfor
Until Min = 0
Return GroupsThời gian thực thi giờ không còn là vấn đề nữa, mà vấn đề giờ đây chính là thuật toán! Và khi ta thử ví dụ 0 trong bài, thuật toán của chúng ta trả về kết quả là 4 chứ không phải là 5. Nhưng kết quả trả về trong ví dụ 1, 2 và 3 thì lại đúng. Đối với ví dụ cuối cùng, thay vì tạo ra 3983180234 nhóm, ta chỉ tạo được 3983180207 nhóm mà thôi. Bằng việc chỉ sai lệch chút ít, ta có thể thấy rằng giải thuật của mình khá tốt, thế nên giờ ta chỉ cần cải tiến nó theo hướng này.
Cho đến hiện tại, ta đã có trong tay hai thuật toán: * Thuật toán tham lam đầu tiên chính xác, nhưng không đủ nhanh. * Thuật toán tham lam thứ hai nhanh, nhưng lại không chính xác.
Giờ, điều mà ta cần làm đó chính là tăng độ chính xác của thuật toán này lên nhiều nhất có thể, mà thời gian thực thi vẫn không bị quá giới hạn. Một cách cơ bản, ta đang tìm kiếm sự cân bằng giữa thời gian thực thi và độ chính xác. Điểm khác biệt duy nhất giữa hai thuật toán kể trên chính là số lượng nhóm mà chúng ta lựa chọn được. Chúng ta sẽ có một phương án như sau: ta sẽ lựa ra một số lượng lớn nhóm ngẫu nhiên lúc đầu, sau đó sẽ giải quyết đoạn còn lại theo cách tiếp cận an toàn hơn. Khi mà chúng ta chỉ còn lại một số lượng nhỏ người dân chưa được phân nhóm ở các quốc gia, thì lúc này nó hoàn toàn hợp lí khi ta sử dụng phương pháp vét cạn. Với biến Allowed được khỏi tạo trong thuật toán dưới đây, ta điều khiển số lượng nhóm mà ta mong muốn tạo tại thời điểm được cho.
Groups = 0
Repeat
// sắp xếp lại mảng theo thứ tự giảm dần
Sort (A)
Min= A[K]
Allowance = (Min+999) / 1000
Groups = Groups + Allowance
For I = 1 to K
A[I] = A[I] - Allowance
Endfor
Until Min = 0
Return GroupsTổng kết
Tham lam thường dễ nghĩ ra, dễ thực thi và thời gian thực thi rất nhanh. Để chúng minh rằng thuật Tham lam là đúng đôi khi cần phải dùng tới các kiến thức toán học chuyên sâu và thường thì việc chứng minh vô cùng khó. Ngoài ra, Tham lam còn thường được dùng để gian lận. Chỉ cần thiếu đi dù chỉ là một chi tiết rất nhỏ thì nó đã đủ làm đòn chí mạng cho thuật toán của bạn rồi. Nhưng khi bạn chẳng có thứ gì trong tay, thì nó quả thực là một sự cứu rỗi. Khi sử dụng quay lui hoặc quy hoạch động, nó giống như bạn đang di chuyển trên mặt đất an toàn. Còn đối với tham lam, thì nó giống với việc đi trên một bãi mìn hơn. Mọi thứ trên bề mặt có vẻ ổn, nhưng khi phần được chôn giấu dưới mặt đất có thể phát nổ ngay khi mà bạn ít ngờ tới nhất. Ngoại trừ một số thuật toán được tiêu chuẩn hóa, thì các phần lớn các bài toán được giải theo phương pháp này được gọi là heuristics. Thật sự nó không tồn tại một công thức chung nào cho việc áp dụng Tham lam vào các bài toán cả, tuy nhiên, sự phân tích các bài toán có thể cho ta một tầm nhìn sáng suốt. Những khái niệm toán học cao cấp như matroids có thể đưa đến cho bạn những công thức toán học để chứng minh các lớp bài tập có thể giải bằng Tham lam, nhưng sau cùng thì những ý tưởng Tham lam cũng chỉ đến từ trực giác và kinh nghiệm của các lập trình viên. Trong một vài trường hợp, có rất nhiều giả định Tham lam nhưng chỉ vài trong số chúng là thực sự chính xác (xem Bài toán "Lựa chọn hoạt động"). Mặt khác, đối với các bài toán khó, thường luôn có một cách giải tắt bằng việc khéo léo trong sử dụng Tham lam, giống như trường hợp của bài tập cuối cùng mà ta vừa đề cập, WorldPeace. Và đây chính là toàn bộ vẻ đẹp của thuật toán Tham lam! Không cần phải nói, nó mang đến những cơ hội thử thách vô cùng hấp dẫn ...
Một vài lưu ý nhỏ
Nhưng bài tập mà có vẻ cực kỳ phức tạp (như TCSocks) có thể xem như là dấu hiệu để tiếp cận bằng phương pháp Tham lam.
Nhưng bài toán mà dữ liệu đầu vào rất lớn (mà kể cả thuật toán có độ phức tạp $O(n^2)$ vẫn không kịp) thường được giải bằng tham lam hơn là quay lui hoặc quy hoạch động.
Mặc dù nó có vẻ rùng rợn, nhưng bạn nên nhìn thuật toán tham lam dưới đôi mắt của một thám tử chứ không phải là dưới cặp kính của một nhà toán học.
 Một thám tử giỏi tham lam.
Một thám tử giỏi tham lam.
 Một người tham lam may mắn.
Một người tham lam may mắn.
 Một người tham lam không may mắn.
Một người tham lam không may mắn.
- Ngoài ra, việc học tập một số thuật toán có sử dụng Tham lam sẽ giúp nắm vững phương pháp này hơn (thuật toán Prim, thuật toán Kruskal, thuật toán Dijkstra)
Bài tập mở rộng
Cấp độ 1
GroceryBagger – SRM 222
FanFailure – SRM 195
PlayGame – SRM 217
SchoolAssembly – TCO04 Round 2
RockStar – SRM 216
Apothecary – SRM 204
Boxing – TCO04 Round 3
Unblur – TCO04 Semifinal Room 3
Cấp độ 2
Crossroads – SRM 217
TCSocks – SRM 207
HeatDeath – TCO04 Round 4
BioScore – TCO04 Semifinal Room 1
Rationalization – SRM 224
Cấp độ 3
GoldMine – SRM 169
MLBRecord – TCO04 Round 2
RearrangeFurniture – SRM 220
WorldPeace – SRM 204